Causal Inference to Ascertain Causes of Metastasis in Melanoma

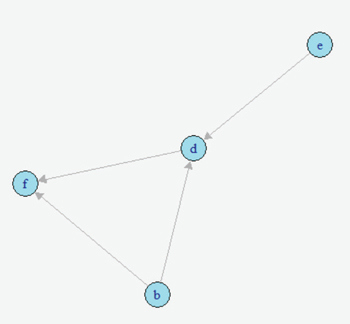
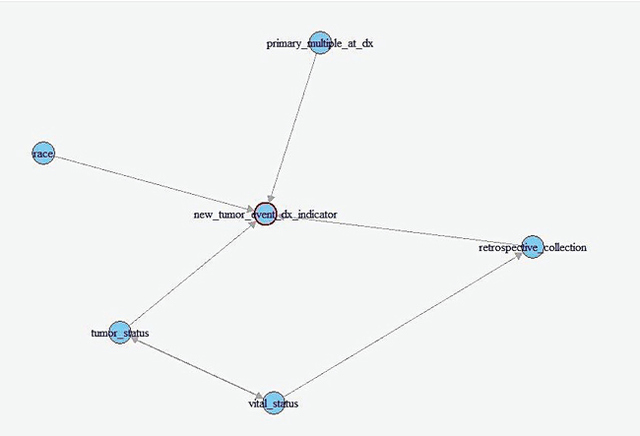
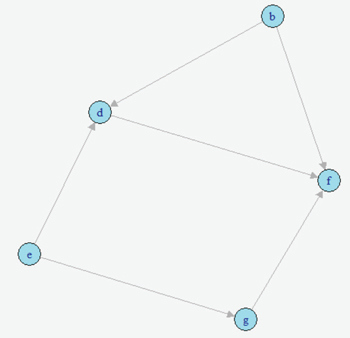
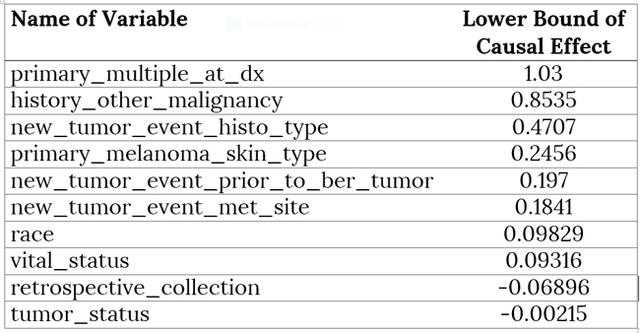
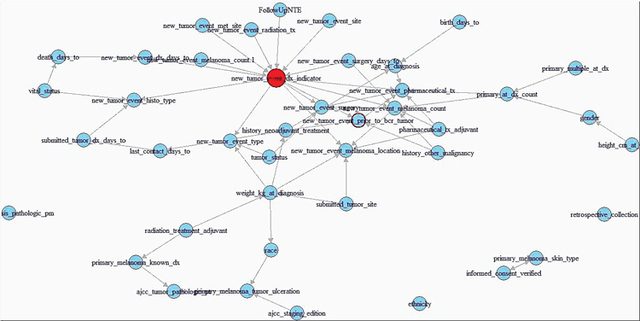
Introduction

Understanding the causes of metastasis in cancer is an important task in cancer medicine. Despite decades of research focusing solely on the genetic events implicated in the metastatic pathway, the actual causes of metastasis remain a mystery (Fidler, 2003; Gupta & Massagu, 2006). In cancer medicine, the current definition of metastasis is the growth of tumor cells that have become detached from the primary tumor, which is a fairly precise one. Recent work has shown that there is a strong genetic component.

As of 2006, metastasis remains the primary cause of death from cancer, causing approximately nine-tenths of all cancer deaths (Martinez, 2006). Looking solely at the statistics of bone metastasis, it is estimated that 350,000 people die each year from metastasis. A similar issue affecting the importance of metastasis is pain. Metastases, especially those in the brain and bone, are rarely silent in nature and quite often cause intractable pain in the bones themselves (Mundy, 2002). For both the clinician and the patient, understanding the causes of metastasis is important.

Skin cutaneous melanoma (SKCM) is a cancer affecting melanin-producing cells in the skin. It is a fairly common type of cancer with approximately 70,000 new cases diagnosed each year. Unlike many other cancer types, it has a fairly high survival rate with only approximately 8,000 deaths each year (The Cancer Genome Atlas, 2015). Similarly, many melanomas are diagnosed only after metastasis because many of those melanomas stay on the skin or other pigmented tissues and never metastasize. Much of the research regarding this disease has recently focused on attempting to understand and predict metastasis of this type of cancer. In The Cancer Genome Atlas (TCGA) project, most of the research has been done on cases that have metastasized. This approach allows for a fairly interesting dataset which has several observations that are related to metastasis, including ample observations that include metastatic tumors.

With regard to SKCM, metastases are particularly notable for several reasons. First, these metastases often spread throughout the body. Often these metastases spread to bone, causing immense pain for the patient, or to other vital organs where the metastases can result in death (Martinez, 2001; The Cancer Genome Atlas, 2015). Second, melanoma that does not metastasize often has minimal negative effects and can linger on the skin undiscovered. Thus, research to ascertain the causes of the transformation of a non-metastasized melanoma to a metastasized melanoma is relevant and clinically motivated.

Causal inference techniques are increasingly used in research as an alternative and enhancement of traditional statistical techniques. Causal inference is used to gain more detailed knowledge about treatments and effects rather than just simply measuring associations (Hernans & Robins, 2016; Pearl, 2009). Techniques for causal inference, though strongly developed, are actually used much less frequently than other statistical measures. For example, while there are many studies that have developed measures of mutational importance to phenotypes in cancer, none of them attempt to address the problem from a causal standpoint (Ramazzotti et al., 2014; Korsunsky et al., 2014; Stingo et. al., 2014; Zhang et al., 2014; Neapolitan et al., 2014). In the field of cancer biology, these uses of different causal inference techniques are novel.

"...the current definition of metastasis is the growth of tumor cells that have become detached from the primary tumor."

In this project, the primary dataset for causal inference comes from the TCGA project's collection of clinical and new tumor event records for SKCM (The Cancer Genome Atlas, 2015). The dataset was assembled by adding together varying clinical data files. After adding together different datasets, a new dataset was compiled that contained 504 records for 71 different clinical observations. This approach results in a very high-dimensional observational dataset that may drastically increase the challenges for accurately utilizing causal inference techniques in order to understand the causes of metastasis.

Development of the causal graph.

Much of the work surrounding causal inference depends on the development of a causal directed acyclic graph (DAG) that describe the causal situation in the real data. Recently, several algorithms have been used to solve this problem and to attempt to infer these DAGs solely from observational data. This project utilized the PC algorithm originally developed by Peter and Clark (Spirtes, Glymour, & Scheines, 2000), and later implemented and refined by Kalisch and then Maathuis (Kalisch & Bühlmann, 2007; Maathuis et al., 2007).

However, this method also has several flaws. It bears noting that no algorithm can ever learn the exact structure of the causal graph from the data itself due to the fact that different graphs can have the same likelihood score and cannot otherwise be differentiated. Similarly, the PC algorithm also assumes that any correlations between data points that are not linked in the graph are solely due to the interactions of the other variables in the graph (conditional independence). Next, we must also assume that all of the variables in the data are Gaussian random variables that follow the conditional independence assumption above. The final primary assumption is the sufficiency condition, which states that there are no hidden variables related to the data that could potentially have a causal influence on any of the variables in the data set (Shalizi, 2013; Murphy, 2012). This assumption must exist for this project to occur, and its potential invalidity is in the "Discussion" section.

The PC algorithm consists of two separate parts. The first step of the algorithm is often called the PC algorithm, which maximizes the probability of the skeleton (undirected edges) of the causal graph for a certain amount of time. This probability is determined by iteratively finding different potential neighbors and testing them for conditional independence. The second step of the algorithm determines the direction of the edges via testing independence of triples that are defined as pairs of nodes with a common neighbor. The end result of this algorithm is an equivalence class of DAGs that have estimated directed edges (Colombo et. al., 2012).

Although the algorithm itself is fairly complex, the results are easy to interpret. The output of this algorithm is a causal graph that has been tested for independence. Similarly, in building an implementation of this algorithm in R, Maathuis showed its accuracy on both simulated data derived from a multivariate normal distribution and real-world gene expression data from a model organism (Murphy, 2012; Maathuis, Colombo, Kalisch, & Bühlmann, 2010).

Methods

After generating the estimated causal graph, different methods were performed for finding the causal effects of different variables in the causal graph on metastasis.

Definition of causal effect.

First, it is necessary to define what a causal effect actually is. Perhaps the simplest measure of any causal effect, the average causal effect (ACE), can be described as:

Y is treated as the outcome variable and a as the treatment variable with two levels. In a population with possible different levels, this can be written in terms of expectations, such that:

Here, one should note the different notation being used–this is a counterfactual variable and not necessarily a variable that measures reality. This counterfactual expectation measures not the expected value of Y given the treatment a, but rather the expectation of the entire population if the entire population were given the treatment (Hernans & Robins). This treatment of a causal effect is just one of multiple methods of defining causal effects. A second one, developed by Judea Pearl, includes the usage of do-calculus (Murphy, 2012).

At its most basic level, causal inference requires three assumptions: consistency, positivity, and exchangeability. In order to causally inference, it is first necessary to assume consistency, which, as stated by Hernan and Robins, is "the outcome for every treated individual ... [is]... his outcome if he had been treated and the outcome for every untreated individual ... [is]... his outcome if he had remained untreated." Under consistency, it is possible to assume that the versions of treatment are equal; it allows relation of counterfactual to the real value (Hernans & Robins). In the SKCM dataset, consistency of all treatments is required to be assumed in order for any meaningful analysis to be done. It does seem like this is a justified assumption, as the questionnaires that were used to generate the data are fairly straightforward. Next, the positivity condition requires that there must be a treatment level greater than zero for all treatment levels being analyzed. While this does seem trivial at first glance, it can become problematic in the real world (Hernans & Robins). In the SKCM dataset, the data was first cleaned in order to give the conditions for positivity.

The exchangeability condition requires that, in a population, the probability of the treatment is independent of the outcome (i.e. untreated individuals would have the same outcomes as those treated, had they also been treated). It cannot be expected to hold in observational studies in its broadest form, but most causal inference methods allow for the more narrow conditional exchangeability to hold (the same outcomes would result for the untreated being treated given confounding and effect modifying variables). For any real meaningful analysis to be done, it was necessary to assume this condition also holds for the SKCM dataset.

IDA method

On purely observational data, it may be impossible to get completely accurate causal effects. This is mostly due to the fact that there are always confounding variables and that, like the trite statistics adage, an associational effect may not actually estimate the true causal effect (Hernans & Robins). However, different methods exist for estimating the causal effect on purely observational data.

One such method is the Iterative Deepening A* algorithm, or IDA (Maathuis et al., 2007). This algorithm describes the possible causal effect among all different DAGs in the set of equivalent DAGs that describe the dataset in question. The term IDA is short for "intervention calculus when the DAG is absent" and was originally developed to infer the causal effect of gene deletions on phenotype (Maathuis, Colombo, Kalisch, & Bühlmann, P., 2010)

Although the exact details of this algorithm are out of the scope of this project, the algorithm works on a fairly simple procedure. For each possible graph in the set of equivalent graphs in the class, it utilizes a simple regression procedure in order to gain an estimate of the causal effect of a treatment a on an outcome Y. The exact value returned is the minimum calculated effect of all of the equivalent graphs. This value can be shown to be the minimum value for the causal effect of a on Y (Murphy, 2012; Bühlmann, 2013).

Validation: other causal inference methods.

The IDA method requires validation in order to ensure that it was both estimated properly and that its output makes sense. DAG were constructed on the SKCM dataset and running the implementation of IDA on this dataset. The top six nodes estimated to have the highest minimum causal effects were taken and modelled using instrumental variable analysis and marginal structural models. In addition, outcome regression was done for the modelings.

"The causal effect of tumor status on the event of metastasis is actually fairly small."

Instrumental variables.

Implementing instrumental variables is a relatively widespread method of performing causal inference in the presence of confounding variables (Cameron & Trivedi, 2005). In Figure 1, an instrument, e, for understanding the effect of d on f in the presence of the confounding variable b was implemented. One unbiased estimator can then be described in terms of covariances with respect to the instrument e. Thus, the estimated causal effect of d on f is estimated by the following equation:

Figure 2 represents a more complex case, where there is the front-door path from e to f via g. Thus, determination of the causal effect of d on f using the instrumental variable b would require conditioning on g, which is easily accomplished.

Marginal structural models.

Marginal structural models are another method of causal inference on smaller datasets which were also implemented. A very simple marginal structural model on a population has the form of the following:

This is regression on a counterfactual and requires a pseudopopulation or IP-weighting on the values of a in order to make correct predictions. IP-weighting is another procedure that estimates the weights of the population by finding the probability distribution of the treatment of A and dividing it by the probability distribution of P(A|L), where L is any other set of covariates in the model. It can also be shown that β 1 is a consistent estimator of the ACE, which shows its usefulness (Hernans & Robin).

"Notably, having a history of other malignant tumors and specific skin types for melanoma both have a significantly greater lower bound on causal effects."

Results

After merging the dataset for the SKCM data downloaded from the TCGA project analysis was begun by utilizing the implementation of the PC algorithm in the R package pcalg (Kalisch, Mächler, Colombo, Maathuis, & Bühlmann, 2012).

Since the only tuning parameter is the significance level of the edges, multiple different parameters were tested. However, utilizing a low significant level resulted in a DAG with too few connections. Thus, the utilized significance level was determined to be .25, which is high but still yielded in accurate results. The resulting estimated DAG is shown in Figure 3.

The next step after generating the estimated causal DAG was to run the IDA algorithm to estimate lower bounds on the causal effects for all correlates on metastasis. This was done using the pcalg package in R. The estimated lower bounds of the causal effects for the largest, positive nine correlates as well as two other interesting negative correlates are shown in Table 1. Many of the correlates that IDA calculated to have a large causal effect are actually metastasis specific.

Five of these variables including primary multiple at diagnosis, race, vital status, and tumor status were then chosen to further validate the bound analysis. Notably, having a history of other malignant tumors and specific skin types for melanoma both have a significantly greater lower bound on causal effects. Many of the correlates that IDA calculated to have a large causal effect are actually metastasis specific.

Next, the same PC algorithm was used on the identified of clinical correlate subset to better understand this relationship between the correlates. The result of the algorithm's analysis is shown in Figure 4. Next, marginal structural models and instrumental variables on this DAG class were used in order to verify the results. In the marginal structural models, IP-weighting is applied to measure a pseudo-population across the other covariates. The results of this causal effect is shown in Table 2.

"First, the IDA* algorithm is a fairly accurate and useful tool in identifying the causal relationships between different nodes."

Finally, vital status (binary: 0=alive, 1=dead) was used as an instrument for estimating the causal effects that both tumor status at recording time and the retrospective collection indicator have on metastasis. Due to the front-door paths in the DAG for tumor status and retrospective collection, when calculating the instrumental variable estimator, it was necessary to condition the algorithm to block those paths. The causal effect of tumor status on the event of metastasis is actually fairly small. This result is verified by the fact that many metastases do not result in death but instead require surgery to remove both the metastasis and the primary tumor. The retrospective collection indicator also shows that the TCGA Project did not choose a random sample of SKCM patients when collecting data for this survey, but rather a sample of SKCM patients that were biased towards metastasis. Although these results are larger than the values calculated by the IDA algorithm, they do seem to agree overall.

Discussion

Using causal inference methods on this set of clinical correlates for SKCM does give some interesting results; however, much of the data do seem to depend on each other, which dampen the results. For example, three of the eight highest values of estimated lower bounds on causal effects that were found from the IDA algorithm exist only in cases of metastasis. Although the methods implemented in the study may have worked correctly, this is in reality a reversal of causal effect (metastasis would cause these other variables to change, rather than the reverse) that is simply an artifact of the data.

"Looking at the data itself, having multiple primary tumors at the time of diagnosis seems to be a cause of metastasis at a later time."

Although the results for this project were ultimately unsatisfactory in determining interesting possible causes of metastasis in SKCM, there are multiple interesting conclusions that can be drawn from the work. First, the IDA algorithm is a fairly accurate and useful tool in identifying the causal relationships between different nodes. Although the IDA algorithm only determines a lower possible bound on the causal effect, it did seem to correctly identify the relationship between the Primary Multiple Tumors Status indicator and Metastasis. Similarly, most of the connections in the full DAG potentially made sense. Another validation measure that the IDA algorithm passed was in having effects that did survive in other more-established measures for causal inference. Secondly, there does seem to be a clinical relationship between having multiple primary tumors and eventually having a metastasis event. Looking at the data itself, having multiple primary tumors at the time of diagnosis seems to be a cause of metastasis at a later time. Further work is necessary to adequately make this conclusion, determine the validity of the results, and establish if this relationship is actually just an artifact of the way that the TCGA clinical patient data is structured. The TCGA data dictionary suggests that this is not actually an artifact. Since multiple melanomas can be known to develop at the same time, this relationship may just show the increased probabilistic risk for metastasis if a patient has multiple melanomas. For example, a patient with multiple melanomas at different sites on their body would have an increased risk for at least one of these melanomas to metastasize. This fact seems to be understood among clinicians but has not been empirically proven before (Martinez, 2001).

Finally, the validity of these methods shows that this type of analysis can be extended to include more than just the clinical features of the tumor. The TCGA Project did not only collect the clinical features of these tumors, but also sequenced the DNA of either the metastatic tumor or the primary tumor in the same patients. The sequencing data as well as multiple other data types is also publicly available. or future work in this direction, integrating variants identified either from DNA sequencing (genome) or in mRNA sequencing (transcriptome) could be integrated into the causal DAG. This may actually allow for more accurate identification of driver and passenger mutations in melanoma (and other cancers), which is a large field of current research (Greenman et. al, 2007). This type of integration may also allow for a more accurate understanding of the genetic causes of metastasis. Further research could also attempt to integrate data of multiple types for example the type of clinical data used in this project, as well as both genome and expression data collected from the TCGA Project.

Author

Wesley is a current third-year student studying Systems Biology at Case Western Reserve University and will be pursuing an MS in Statistics in the Integrated Graduate Studies Program in the fall.

Acknowledgements

The results shown here are in whole based upon data generated by the TCGA Research Network. I would also like to acknowledge Dr. Andy Podgurski for teaching EECS 442: Causal Learning from Data from which this research emerged as a final project. Finally, I would like to acknowledge Drs. Thomas LaFramboise and Sneha Grandhi for giving me access to the clinical dataset that was used in this project.

References

Bühlmann, P. (2013). Causal statistical inference in high dimensions. Mathematical Methods of Operations Research, 77(3), 357–370. doi:10.1007/ s00186-012-0404-7

Cameron, A. C., Trivedi, P. K. (2005). Microeconometrics: methods and applications. Cambridge University Press.

Colombo, D., Maathuis, M. H., Kalisch, M., & Richardson, T. S. (2012) Learning high-dimensional directed acyclic graphs with latent and selection variables. The Annals of Statistics, 40(1), 294–321. doi: 10.1214/11-AOS940

"Cutaneous Melanoma–TCGA." Available: http://cancergenome.nih.gov/cancersselected/melanoma

Fidler, I. J. (2003). The pathogenesis of cancer metastasis: the "seed and soil" hypothesis revisited. Nature Reviews Cancer 3(6): 453-458. doi:10.1038/ nrc1098

Greenman, C., Stephens, P., Smith, R., Dalgliesh, G. L., Hunter, C., Bignell, G. et al. (2007). Patterns of somatic mutation in human cancer genomes. Nature, (446)7132, pp. 153-158. doi:10.1038/nature05610

Gupta, G. P. & Massagu, J. (2006). Cancer metastasis: building a framework. Cell 127(4), pp. 679-695. doi:10.1016/j.cell.2006.11.001

Hernan, M. & Robins, J. (2009). Causal inference. Boston: Chapman & Hall. Kalisch, M., & Bühlmann, P. Estimating high-dimensional directed acyclic graphs with the PC-algorithm. The Journal of Machine Learning Research, 8, 613-636, 2007.

Kalisch, M., & Bhlmann, P. Estimating high-dimensional directed acyclic graphs with the PC-algorithm. The Journal of Machine Learning Research, 8, 613-636, 2007.

Kalisch, M., & Bhlmann, P. Estimating high-dimensional directed acyclic graphs with the PC-algorithm. The Journal of Machine Learning Research, 8, 613-636, 2007.

Kalisch, M., Mächler, M., Colombo, D., Maathuis, M. H., & Bühlmann, P. (2012). Causal inference using graphical models with the r package pcalg. Journal of Statistical Software, 47(11), 1-26. doi: 10.18637/jss.v047.i11

Korsunsky, D., Ramazzotti, D., Caravagna, G., & Mishra, B. (2014) Inference of Cancer Progression Models with Biological Noise. arXiv. doi: 10.1101/008326

Maathuis, M. H., Colombo, D., Kalisch, M., & Bühlmann, P. "Predicting causal effects in large-scale systems from observational data," Nature Methods, 7(4), 247-248. doi: 10.1038/nmeth0410-247

Maathuis M. H., Kalisch, M., & Bühlmann, P. Estimating high-dimensional intervention effects from observational data. The Annals of Statistics, 37(6), 3133-3164. doi: 10.1214/09-AOS685

Martinez, J. C. & Otley, C. C. (2001). The management of melanoma and nonmelanoma skin cancer and a review for the primary physician. In Mayo Clinic Proceedings. Elsevier 76: 1253-1265. doi: 10.4065/76.12.1253

Mundy, G. R. Metastasis: Metastasis to bone: causes, consequences and therapeutic opportunities. Nature Reviews Cancer, 2(8), 584-593. doi: 10.1038/ nrc867

Murphy, K. P. (2012). Machine learning: a probabilistic perspective, ser. Adaptive computation and machine learning series. MIT Press.

Jiang X, Xue D, Brufsky A, Khan S, Neapolitan R. (2014). A New Method for Predicting Patient Survivorship Using Efficient Bayesian Network Learning. Cancer Informatics. 13:47-57. doi:10.4137/CIN.S13053

Ni Y, Stingo FC, Baladandayuthapani V. (2014) Integrative Bayesian Network Analysis of Genomic Data. Cancer Informatics. 13(Suppl 2):39-48. doi:10.4137/ CIN.S13786.

Pearl, J.J. (2009). Causal inference in statistics: An overview. Statistics Surveys, 3, 96-146. Available: http://projecteuclid.org/euclid.ssu/1255440554

Ramazzotti, D., Caravagna, G., Loohuis, L. O., Graudenzi, A., Korsunsky, I. Mauri, G., Antoniotti, M., & Mishra, B. Efficient inference of cancer progression models. arXiv. doi:10.1093/bioinformatics/btv296

Shalizi, C. R. Advanced data analysis from an elementary point of view. Preprint of book found at http://www.stat.cmu.edu/cshalizi/ADAfaEPoV

Spirtes, P., Glymour, C. N., & Scheines, R. (2000). Causation, prediction, and search. MIT press, 81.

TCGA Data Portal, National Institutes of of Health. Received from https://tcgadata.nci.nih.gov/docs/dictionary/

Zhang, Q., Burdette, J. E., & Wang, J. P. (2014). Integrative network analysis of TCGA data for ovarian cancer. BMC Systems Biology, 8(1). doi:10.1186/s12918014-0136-9