The Implausibility of the Barter Narrative & Credit Money in Ancient Babylon

IV. Credit and Barter – Historical Difficulties

The problem with evaluating whether money ever emerged according to the barter narrative is that the conditions a historical society would have to meet to be a barter economy are strict already, and the three function definition of money excludes devices, like credit, which solve some of the essential problems but are not themselves media of exchange. Evidence proving the barter narrative would have to show two things:

1. An economy dominated by barter, meaning direct simultaneous exchange of goods;
2. The emergence of a commodity in that economy which fulfills the unit of account and store of value function, but removed the coincidence of wants problem through the medium of exchange function.

Of these two requirements perhaps the hardest one to substantiate historically is that a barter economy based on simultaneous direct exchange ever existed.

"Barter is at once a cornerstone of modern economic theory and an ancient subject of debate about political justice, from Plato and Aristotle onwards. In both discourses, which are distinct though related, barter provides the imagined preconditions for the emergence of money. Why should anthropologists be interested in logical deductions from an imagined state? No example of a barter economy, pure and simple, has ever been described, let alone the emergence from it of money; all available ethnography suggests that there never has been such a thing. Nevertheless, there are economies today which are dominated by barter" – Humphrey, 1985

While there have certainly been societies that used barter, there are no examples of economies relying on barter for trade between neighbors. Barter ordinarily "takes place between strangers, even enemies"( Graeber, 2011). In a way, barter is an extreme case of credit where the loan is repaid instantly. For interactions between family members or neighbors, there is no need for this kind of strict requirement since debts can be repaid in a variety of ways over a flexible time span. Between strangers and enemies however, each party must be wary that the other is not going to murder, steal, or both. Barter is thus ritualized, and pushed into the margins of societal activity.

V. Four Merchant Model

Using four players in a simple connected network, a variety of outcomes relevant to the functions of money can be demonstrated. One important result is that using a system of credits (loans) no more complex than those written onto clay tablets in the Ur III dynasty of Old Babylon (2000 1600 BC), it is possible to gain all three functions of money. The loan contract by definition fulfills the unit of account function and is a store of value, and when traded becomes a medium of exchange. This is particularly relevant to the barter story because while there are no historical economies based around barter as a primary mode of exchange, ancient Babylon contained a wealth of sophisticated banking operations inside their temples, leading to a widespread use of contract loans throughout the society and the legal codification of contract law to go with it. The model that follows uses four merchants in a network structure because it is relatively simple to model the standard problems with barter, the use of credits to solve them, and can be used to simply analyze the profitability of becoming a middleman due to the complementarity of the goods being traded.

VI. Model Overview

There are four producers of goods in a primitive economy, situated in a circle around a treacherous mountain. In their native tongue they are named after what they produce (the grain producer is named ‘Grain', and so on). Each player can talk only to a neighbor a quarter of the way around the mountains: the mountains permit noone to pass them and thus it is impossible for a player to either communicate or enforce contracts with the player opposite (over the mountains, see fig. 5 ). Each player specializes in the production of a specific unit goods vector: W,G, B or S. For instance, when Wood makes a unit of output I refer to it as W = (1, 0, 0, 0). Similarly, when he produces x units of output, I refer to it as xW = (x, 0, 0, 0).

Now, for simplicity take the case of homogeneous preferences. Let the utility of every producer be dependent on their holdings vector h = (h₁, h₂, h₃, h₄) in the same way:

 

The benefits of this utility function are that (1) it is easy to compute and (2) it fulfills the usual conditions of utility:

 

VII. Barter solution

The lack of communication over the mountins doesn't hinder a paretooptimal outcome if there is, in addition to homogeneous preferences, homogeneous production. Given that no producer has any preference for any particular good, and each starts out with the same amount a of their specialized resource – Wood has aW, Grain has aG etc. – an efficient allocation (which is also very egalitarian) can be reached in four trades:

1. Wood, holding aW, knows that Grain holds aG and that Sheep holds aS. Since goods are preferred equally, Wood is indifferent to a trade with Sheep or a trade with Grain. Given that one is chosen, trading must commence until there are no pareto improving moves left. It is easy to see if Wood chooses Grain, he gives her (a/2)W in exchange for (a/2)G in return.
2. Next, noticing that a similar situation would occur between the sheep and brick producers: Brick gives Sheep (a/2)B in exchange for (a/2)S in return.
3. Now that Wood has (a/2)[W + G] and Sheep has (a/2)[B + S], Wood can give Sheep (a/4)[W + G] for (a/4)[B + S] in return.
4. Similarly, Grain can give brick (a/4)[W + G] for (a/4)[B_r + S_h] in return.

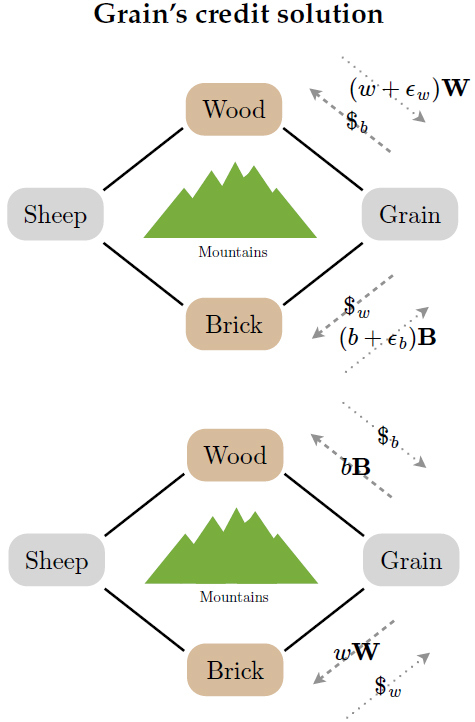
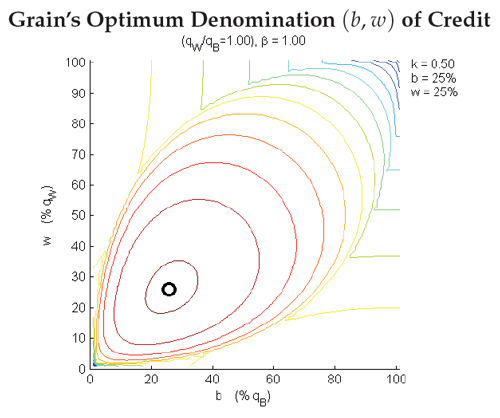
At the end of these four trades, each player holds and is able to consume h_f = (a/4, a/4, a/4, a/4). This final allocation yields

 

as compared with the utility of the initial allocation

The barter solution gives a factor of 2^2−ka^k higher utility, which is an improvement since k ϵ 2 (0, 1) ⇒ 2^2−ka^k > 1. This has some nice features. When marginal utility diminishes quickly, i.e. when k is close to zero, the gains from this kind of trade are very high and utility can be increased for every player asymptotically up to four times its original level.

Implications and features of barter without money

The barter case described above includes no media of exchange, no units of account, and no stores of value. Despite this, the result of this trading is optimal in a utilitarian sense. Given (a, a, a, a) to distribute among four players, one could not have done better in terms of total utility. In addition, every good made its way around the mountains by a sequence of mutually agreeable trades. In this situation there can be no role for money to play. The usual objections to barter: transaction costs, double-coincidence of wants (Jevons, 1875), and identification costs (Alchian, 1977), don't apply as everyone is always willing and able to trade something with their neighbor to facilitate trade.

"In real life, of course, things are more complicated; we are ‘awash' in trading intermediaries because we cannot easily discover and exploit potential gains from trade without them." – Clower, 1995

If we were to keep homogeneous preferences but get rid of homogeneous production, barter would fall apart.

VIII. Borrowing Solves a Broad Class of Trading Problems

One way we can easily see how money may arise as a unit of account is to imagine that our land is hit by a drought, and no sheep or wheat can be produced. In this situation, though units of brick may highly valuable to everyone, there's no way for anyone to obtain benefits from trade using a traditional scheme of sequential transactions. In this system, every trade must be improving to both players, and since in a ‘primitive' world there's no notion of credit (yet), there's no incentive for Brick or Wood to trade with Grain and Sheep. Suppose that Grain creates the world's first promissory notes specifying on a clay tablet – as was done in Babylonian times – a debt of some number w units of wood to be paid to the bearer of the clay tablet. Suppose also that she creates another tablet denoting a debt of some number b units of brick. For the sake of convenience, I denote the tablet with debt in terms of w units of wood as $w, and the tablet with debt in terms of b units of brick as $_b.

Now, if Grain completes a trade of $_b for (w + ϵ_w)W with Wood, and a trade of $_w for (b + ϵ_b)B with brick, then she can redeem her tablets by giving Wood bBr and Brick wW_o. In this way, she keeps ϵ_wW + ϵ_bB for herself.

Merchant profits using the functions of money

By utilizing credit in a clever way, Grain has become the worlds first money-wielding merchant. This form of trading can make use of every aspect of money as defined by Hicks (1967): all that's required is to say that some time has passed between the issuing of the promissory notes and the claiming of the goods written in the contracts. As a medium of exchange, the promissory notes fulfill a role as an intermediate good solving the double coincidence of wants problem, albeit in a closed loop. Grain – initially – has nothing to offer Brick or Wood, so the coincidence of wants problem exists. By creating what is essentially a unit of account to handle credit, Grain can benefit herself by enforcing contracts with Brick and Wood, even though neither Brick norWood can enforce contracts with eachother

This example shows a common theme in the emergence of commodity-backed monies: when the medium of exchange condition is fulfilled, the unit of account condition naturally follows. That is, when it makes sense to players to use an intermediate in exchange, price ratios and exchange rates therefore originate from the use of that intermediate. For instance, due to the intermediate promissory notes, the exchange rate Brick sees between wood (W) and brick (B) is $_w/(b + ϵ_b), which is a price for wood in terms of Grain's promissory notes⁵. On the other hand, before the trades even took place, the loans were by definition units of account. Therefore, this system of credit-money demonstrates that the taking on of debt to personal gain is a plausible alternative to the double coincidence of wants narrative, which stresses the origin of money in transaction costs alone.

Grain's profit

Without considering any costs of issuing the notes, Grain gains ϵ_wW + ϵ_wB from her scheme. There is a limit however to what can be supported as Grain's profit in this kind of system. The first thing to consider is that for this to work, each player must be at least as well off at the end of the trade. This means that

for all players. In the context of the utility function and example I have been using, if Brick produces ρ_BB every turn and (as is commonly assumed) there is a discount factor of β on consumption in the future, then there are two approaches to determining acceptable trades:

One-Shot Solution

When Grain offers Brick one credit, and doesn't expect to issue in the period following, the only acceptable trades must satisfy:

This implies that Brick is indifferent when

For any pair (b, w), the best possible ϵ_b supported in this trade is

For Wood, the same kind of restrictions hold:

This implies that the utility gained by Grain when she denominates $_b and $_w is

This implies the first order conditions:

As can be clearly seen from the above equations, this is a pretty tangled set of first-order conditions. Therefore, I turn to a numerical solution. First, however, let me consider what happens in steady state.

Steady-State Solution

When Grain gives Brick a note in exchange for (b + ϵ_b)B_r every turn, the trades must satisfy:

This implies that the discount rate β has no effect on the outcome since the (1 + β) can be dropped from both sides. Indifference implies equality and:

Similar to before:

This is to be expected: the steady-state solution is merely the one-shot solution with no discount rate β.

IX. Numerical Solution

As an alternative to the mind-numbing slog of solving the first order conditions, it's convenient instead to simply solve for the maximum profit over a grid of possible (b, w) pairs (equivalent to a numerical solution of the first order conditions). When parametrized in b and w, the level sets of the profit u(π^→) can be plotted and the location of the maximum value found. An example of this numerical solution method can be seen in fig. 3 (below).

This particular optimum trade is convenient to demonstrate, while others will depend more complexly on the specification of k, β and the ratio q_W/q_B. If Wood and Brick start out with their initial holdings of (q_W, 0, 0, 0) and (0, 0, q_B, 0), respectively, and q_W = q_B, then their initial utilities are the same: q^k_W = q_k^B. Since k = 1/2, however, they are both indifferent between their initial holdings and final holdings of (q_W/4, 0, q_B/4, 0):

Since the total amount of each good is preserved, however, this gives Grain an initial holdings of (0, 0, 0, 0) and a final holdings of (q_W/2, 0, q_B/2, 0), yielding a utility √2 times that of either Wood or Brick. Being the middleman definitely paid off for Grain in this case.Continued on Next Page »