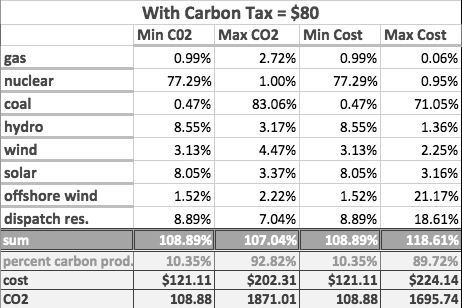
Efficient Pricing of Carbon in the EU and its Effect on Consumers

III. Computational Model

To evaluate the efficacy of the carbon tax on the utilization rates of multiple generation technologies, a computation model was created. The model uses a Monte Carlo process in conjunction with a statistical tool known as the Dirichlet distribution to randomly create an array of portfolios, each with a different share of the various generation technologies. These energy portfolios were then evaluated based on their cost and CO₂ emissions. Certain thresholds were placed on all portfolios to ensure that they were plausible in the real world, namely that a percentage of power was generated from dispatchables (§2.3).

Monte Carlo Simulation

Monte Carlo simulations are often used in modeling in situations where a closed-form analytic solution is not readily available or exceedingly computationally intensive. A Monte Carlo simulation relies on repeated random sampling of input variables to obtain an optimal result. In the case of portfolio management (whether it be energy or equities), by randomly choosing the asset allocation percentages and calculating the costs repeatedly, the law of averages states that as the number of simulations approaches infinity, an optimal solution will be found.

Dirichlet Distribution

In the proposed model, sampling was done according to the Dirichlet distribution, which ensures that some number of points in a set, n, are randomly sampled such that their sum is equal to some specified total. Thus, the Dirichlet distribution has the statistically appealing property of being the conjugate prior to the parameters of the multinomial distribution. In the computational model, the distribution generates N values, bounded by [0,1] that sum to unity.

Dispatchable Reserve Rate

As mentioned in §2.2, grid operators maintain a reserve of dispatchable capactiy based on the fraction of total capacity generated from renewables. Since this is an a posteriori calculation after the desired supply from renewables has been decided, it is calculated in the same manner in the model.

The Dirichlet distribution first creates a portfolio consisting of the generation technologies listed in Figure 7⁶ where the sum of the weights equals 1. Afterwards, an algorithm adds the requisite percentage of dispatchable reserves to the portfolio.⁷ For reserve requirement λ:

Qualification Criteria

Over 20,000 portfolios were generated and stored in a matrix. However, many of these did not meet certain the base load requirement, and were removed. With the remaining portfolios, matrix operations were performed to calculate the cost and emissions. The portfolios that had the highest and lowest cost and CO₂ emissions were then kept for each tax rate.

*Base Load If energy portfolios did not meet a predefined percentage of power generation from dispatchables (ρ), they were culled from the dataset.

All subsequent qualifications (cost and emissions) are done to include the addition of dispatchable reserves to the portfolio.

*Hydroelectric Power Since the amount of power generated from hydroelectric sources is fixed by the number of damable rivers, a limit is placed on the percentage of power that can come from such sources. Research shows that this limit is around 15% of total electric demand.

*Emissions Emissions for each portfolio were calculated by using the weighted average of each generation technology and its respective CO₂ emissions (as described in Figure 7). Where ϵ_i is the CO₂ emissions per MWh of generation technology i, w_i^portfolio_n i is the weight of generation technology i in portfolio_n, and CO₂^portfolio_n is the total CO₂ emissions for portfolio n per MWh.

Costs The costs of each portfolio are tied to the rate at which carbon is taxed and the levelized cost per MWh of each generation technology. Thus, if the portfolio produced more carbon, it would cost more than one that produces less ceteris parabus This is stated mathematically as:

Where costⁿ is the cost of portfolio n and τ is the effective carbon tax rate per tonne of CO₂.

The tax rate τ was systematically increased and cost recalculated for the same 20,000 portfolios until the portfolio with the minimum cost was the portfolio that had the lowest emissions. This tax rate represents the socially optimal tax rate of §1.1.1.

IV. Results

The model yielded a final result that matches well with our intuition of what an 'optimal' energy portfolio would look like: nuclear in the place of coal, a diverse mix of renewables, especially hydroelectric⁸, and supplemental gas turbines for peak demand.

It is my belief that wind power is underrepresented in this model because of its intermittency. If a power grid similar to that explained in §2.3.1 is implemented, the capacity factor of wind on a super national level could theoretically be as high as 80% (Airtricity, 2013)⁹. If the model takes into account this new capacity factor, wind would surely be the dominant resource in the portfolio, as suggested by Gregor Czish in his study of the Supergrid (Claverton Energy, 2009)

It is also important to note that these allocations provided do not take into consideration factors such as geopolitical risk of relying on an extra-national energy supply. The study is also run assuming free market conditions with no government subsidies for nor investment price floors for generated power¹⁰. Perhaps most importantly, the model does not take into consideration the existing energy mix of the EU. Thus, the relative cost of building new nuclear plants would be higher than using the existing gas turbines and simply paying the tax.

In this regard, the model is to be seen as a target for an optimal energy mix of the EU as a whole, not as a blueprint for bolt-on construction.

Optimal Carbon Pricing

The optimal carbon price is defined as the tax rate at which the cost of of producing carbon is equal to the price of using a renewable source. Thus, the optimal carbon tax rate (τ) is found when the portfolio with the lowest cost first becomes the same as the portfolio with the lowest emissions. By this definition, the optimal tax rate is $80 USD per ton of carbon. Past $80, there is a deadweight loss as no more social benefits are produced in the form of cleaner air yet the cost of production– and therefor consumer prices-increases.

As seen above, the optimal mixture is heavily weighted towards nuclear and hydroelectric power. Confirming out intuition of what would constitute a 'dirty' portfolio, the most polluting portfolio uses coal as its primary energy source (83%). In the spirit of the taxation, at a tax rate $80, the most expensive portfolio is also heavily weighted towards coal (71%).

The Effect of Renewables on Consumer Utility Prices

For measures such as the European Supergrid to pass, ultimately the voters will have to approve measures that will raise their taxes. In today's economic climate this will prove difficult, it not impossible, unless consumers can be shown that they will benefit in the medium to long term in the form of lower utility prices. Currently, the average price for electricity in the industrial sector¹¹ in the nations studied is around 97 Euros per MWh (Europe's Energy Portal, 2013). Converted to US dollars at current exchange rates, this price is around $132 per MWh.

Including an average profit margin for utility providers of 3% (Yahoo! Finance, 2013), the cost of the portfolio suggested by this model is $125 per MWh. With a margin of error of plus or minus 5%, these results imply that a Europe with reduced emissions can be achieve at a similar, if not lower, price than currently facing households. The data produced by this model is confirmed by the research of Gregor Czish (Claverton Energy, 2009) If cleaner air won't motivate consumers, surely this will.

V. Future Improvements

This model will be expanded in the future to consider the location of the power plants suggested by this model. Population dynamic considerations such as population density and population growth will motivate the location of power plants, as will physical factors such as line losses from HVDC transport and local distributive capacity.

The future model will also take into consideration the existing mixture of energy resources currently in place in Europe to provide a guideline for which type of power generation the EU should invest in– and in which order– to achieve maximum reduction in emissions at the minimum cost. *

References

1. EIA. "How Much Carbon Dioxide (CO2) Is Produced When Different Fuels Are Burned?"" U.S Energy Information Administration. U.S Energy Information Administration, n.d.Web. 9 Dec.2013.
2. Habb, Tim, and John Whitehead. "Econ 101: Carbon Tax vs. Cap-andTrade." Environmental Economics. N.p., n.d. Web. 9 Dec. 2013.
3. Tashini, Luca, Simon Dietz, and Naomi Hicks. "Carbon Tax v Cap-andTrade: Which Is Better?" The Guardian. N.p., n.d. Web. 9 Dec. 2013.
4. European Commission. "The EU Emissions Trading System." Europa. European Commission, n.d. Web. 9 Dec. 2013.
5. PBS. "Sources of World's CO2 Emissions." Frontline. Public Broadcasting Station, n.d. Web. 9 Dec. 2013.
6. EPA. "Overview of Greenhouse Gasses." EPA. United States Environmental Protection Agecy, n.d. Web. 9 Dec. 2013.
7. UCAR. "How Much Has the Global Temperature Risen in the Last 100 Years?" University Corporation for Atmospheric Research. UCAR, n.d.Web. 9 Dec. 2013.
8. Plumer, Brad. "What Happens if You Add Lots ofWind and Solar Power to the Grid?" The Washington Post. The Washington Post, n.d. Web. 9 Dec. 2013.
9. Wind Energy Center. "Wind Power: Capacity Factor, Intermittency, and What Happens When the Wind Doesn't Blow?" Wind Energy Center. University of Massachusetts Amherst, n.d. Web. 9 Dec. 2013.
10. Puka, Lidi, and Kacper Szuleki. "Plans to Create a Pan-European Electricity Grid as Part of the Common Energy Market Face a Number of Challenges Before They Can be Realised." London School of Economics. LSE, n.d. Web. 9 Dec. 2013.
11. Andrews, Dave. "Why Do We Need The Supergrid, What Is Its Scope And What Will It Achieve?" Claverton Energy. Claverton Energy, 9 June 2009.Web. 9 Dec. 2013.

Endnotes

1. With the exception of fuel cells and photovoltaic which rely directly to the flow of electrons
2. It is important to make the distinction between solar thermal and solar photovoltaic. The former uses solar radiation to heat a working fluid while the later exploits a property of certain materials that causes them to shift polarity when heated
3. Readers familiar with electro-mechanics will recognize this as the duty cycle
4. While technically coal and nuclear are dispatchable, they are more traditionally used to supply base loads since they take more time (days) to ramp up. Aeroderivative gas turbines are the ultimate dispatchable because their production can be started and stopped in a matter of hours.
5. Often cited as "its always windy somewhere"
6. Coal, Nuclear, Natural Gas, Wind, OffshoreWind, Solar, and Hydroelectric
7. This means that the nominal capacity of the grid is always greater than 100% supply
8. Hydroelectric is highly represented because it is has a relatively high capacity factor and is semi-dispatchable. While the maximum output is limited by the flux of water, it can be adjusted down from this maximum by gearing the connection between fan and generator shaft.
9. The Airtricity proposal is heavily weighted towards offshore wind generation which bypasses some of the NIMBY-ism that plagues wind turbine construction
10. Definitely not the case for the EU. In the UK the government has guaranteed that power generated from renewable sources a price of 87 PS per MW, compared to the market price of around 47 PS
11. Industry was used instead of household since it more closely follows the cost of electric production for utility companies. Since the data modeled is based on production, this was deemed prudent.