From The Developing Economist VOL. 2 NO. 1Bayesian Portfolio Analysis: Analyzing the Global Investment Market
By
The Developing Economist 2015, Vol. 2 No. 1 | pg. 1/1
IN THIS ARTICLE
KEYWORDS
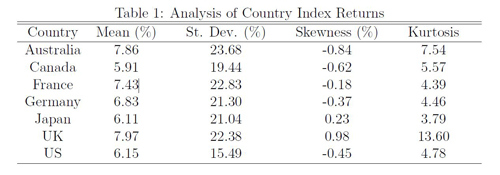
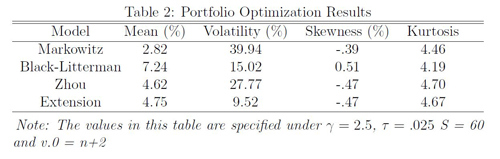
AbstractThe goal of portfolio optimization is to determine the ideal allocation of assets to a given set of possible investments. Many optimization models use classical statistical methods, which do not fully account for estimation risk in historical returns or the stochastic nature of future returns. By using a fully Bayesian analysis, however, I am able to account for these aspects and incorporate a complete information set as a basis for the investment decision. I use Bayesian methods to combine different estimators into a succinct portfolio optimization model that takes into account an investor's utility function. I will test the model using monthly return data on stock indices from Australia, Canada, France, Germany, Japan, the U.K. and the U.S. I. IntroductionPortfolio optimization is one of the fastest growing areas of research in financial econometrics, and only recently has computing power reached a level where analysis on numerous assets is even possible. There are a number of portfolio optimization models used in financial econometrics and many of them build on aspects of previously defined models. The model I will be building uses Bayesian statistical methods to combine insights from Markowitz, BL and Zhou. Each of these papers use techniques from the previous one to specify and create a novel modeling technique. Bayesian statistics specify a few types of functions that are necessary to complete an analysis, the prior distribution, the likelihood function, and the posterior distribution. A prior distribution defines how one expects a variable to be distributed before viewing the data. Prior distributions can be of different weights in the posterior distribution depending on how confident one is in their prior. A likelihood function describes the observed data in the study. Finally, the posterior distribution describes the final result, which is the combination of the prior distribution with the likelihood function. This is done by using Bayes theorem2, which multiplies the prior times the posterior and divides by the normalizing constant, which conditions that the probability density function (PDF) of the posterior sums to 1. Bayesian analysis is an ideal method to use in a portfolio optimization problem because it accounts for the estimation risk in the data. The returns of the assets form a distribution centered on the mean returns, but we are not sure that this mean is necessarily the true mean. Therefore it is necessary to model the returns as a distribution to account for the inherent uncertainty in the mean, and this is exactly what Bayesian analysis does. Zhou incorporates all of the necessary Bayesian components in his model; the market equilibrium and the investor?s views act as a joint prior and the historical data defines the likelihood function. This strengthens the model by making it mostly consistent with Bayesian principles, but some aspects are still not statistically sound. In particular, I disagree with the fact that Zhou uses the historical covariance matrix, Σ, in each stage of the analysis (prior and likelihood). The true covariance matrix is never observable to an investor, meaning there is inherent uncertainty in modeling Σ, which must be accounted for in the model. Zhou underestimates this uncertainty by using the historical covariance matrix to initially estimate the matrix, and by re-updating the matrix with the historical data again in the likelihood stage. This method puts too much confidence in the historical matrix by re-updating the prior with the same historical matrix. I plan to account for this uncertainty by incorporating an inverse-Wishart prior distribution on the Black-Litterman prior estimate, which will model Σ as a distribution and not a point estimate. The inverse-Wishart prior will use the Black-Litterman covariance matrix as a starting point, but the investor can now model the matrix as a distribution and adjust confidence in the starting point with a tuning parameter. This is a calculation that must be incorporated to make the model statistically sound, and it also serves as a starting point for more extensive analysis of the covariance matrix. The empirical analysis in Zhou is based on equity index returns from Australia, Canada, France, Germany, Japan, the United Kingdom and the United States. My dataset is comprised of the total return indices for the same countries, but the data spans through 2013 instead of 2007 like in Zhou. This is a similar dataset to that chosen by BL, which was used in order to analyze different international trading strategies based on equities, bonds and currencies. The goal of this paper is to extend the Bayesian model created by Zhou by relaxing his strict assumption on the modeling of the covariance matrix by incorporating the inverse-Wishart prior extension. This will in turn create a statistically sound and flexible model, usable by any type of investor. I will then test the models by using an iterative out-of-sample modeling procedure. In section II, I further describe the literature on the topic and show how it influenced my analysis. In section III I will describe the baseline models and the inverse-Wishart prior extension. In Section IV I will summarize the dataset and provide descriptive statistics. In section V I will describe how the models are implemented and tested. In Section VI I will describe the results and compare the models, and in Section VII I will offer conclusions and possible extensions to my model. II. Literature ReviewModelsHarry Markowitz established one of the first frameworks for portfolio optimization in 1952. In his paper, Portfolio Selection, Markowitz solves for the portfolio weights that maximize a portfolio?s return while minimizing the volatility, by maximizing a specified expected utility function for the investor. The utility function is conditional on the historical mean and variance of the data, which is why it is often referred to as a mean-variance analysis. These variables are the only inputs, so the model tends to be extremely sensitive to small changes in either of them. The model also assumes historical returns on their own predict future returns, which is something known to be untrue in financial econometrics. These difficulties with the mean-variance model do not render it useless. In fact, the model can perform quite well when there are better predictors for the expected returns and covariance matrix (rather than just historical values). The model by BL extends the mean-variance framework by creating an estimation strategy that incorporates an investor?s views on the assets in question with an equilibrium model of asset performance. Many investors make decisions about their portfolio based on how they expect the market to perform, so it is intuitive to incorporate these views into the model. Investor views in the Black-Litterman model can either be absolute or relative. Absolute views specify the expected return for an individual security; for example, an investor may think that the S&P 500 will return 2% next month. Relative views specify the relationship between assets; for example, an investor may think that the London Stock Exchange will have a return 2% higher than the Toronto Stock Exchange next month. BL specify the same assumptions and use a similar model to Markowitz to describe the market equilibrium, and they then incorporate the investor?s views through Bayesian updating. This returns a vector of expected returns that is similar to the market equilibrium but adjusted for the investor?s views. Only assets that the investor has a view on will deviate from the equilibrium weight. Finally, BL use the same mean-variance utility function as Markowitz to calculate the optimal portfolio weights based off of the updated expected returns. Zhou takes this framework one step further by also incorporating historical returns into the analysis because the equilibrium market weights are subject to error that the historical data can help fix. The market equilibrium values are based on the validity of the capital asset pricing model (CAPM)3, which is not always supported by historical data. This does not render the equilibrium returns useless; they simply must be supplemented by historical data in order to make the model more robust. The combination of the equilibrium pricing model and the investor?s views with the data strengthens the model by combining different means of prediction. As an extension, it would be useful to research the benefit of including a more complex data modeling mechanism that incorporates more than just the historical mean returns. A return forecasting model could be of great use here, though it would greatly increase the complexity of the model. Zhou uses a very complete description of the market by incorporating all three of these elements, but there is one other aspect of the model that he neglects; his theoretical framework does not account for uncertainty in the covariance matrix. By neglecting this aspect, he implies that the next period's covariance matrix is only described by the fixed historical covariance matrix. This is in line with the problems that arise in Markowitz, and is also not sound in a Bayesian statistical sense because he is using a data generated covariance matrix in the prior, which is then updated by the same data. I will therefore put an inverse-Wishart prior distribution on the Black-Litterman estimate of Σ before updating the prior with the data. The primary Bayesian updating stage, where the equilibrium estimate is updated by the investor views will remain consistent. This way Σ is modeled as a distribution in the final Bayesian updating stage which will allow the prior to have a more profound effect. Investment StrategiesThough the Black-Litterman model is quantitatively based it is extremely flexible, unlike many other models, due to the input of subjective views by the investor. These views are directly specified and can come from any source, whether that is a hunch, the Wall Street Journal, or maybe even an entirely different quantitative model. I will present a momentum based view strategy, but this is only one of countless different strategies that could be incorporated, whether they are quantitatively based or not. The results of this paper will be heavily dependent on the view specification, which is based on the nature of the model. The goal of this paper is not to have a perfect empirical analysis, but instead to present a flexible, statistically sound and customizable model for an investor regardless of their level of expertise. The investor's views can be independent over time or follow a specific investment strategy. In the analysis I use a function based on the recent price movement of the indices, a momentum strategy, to specify the views. The conventional wisdom of many investors is that individual prices and their movements have nothing to say about the asset's value, but when the correct time frame is analyzed, generally the previous 6-12 months, statistically significant returns can be achieved (Momentum). In the last 5 years alone, over 150 papers have been published investigating the significance of momentum investment strategies (Momentum). Foreign indices are not an exception, as it has been shown that indices with positive momentum perform better than those with negative momentum (AQR). The basis of momentum strategies lies in the empirical failure of the efficient market hypothesis, which states that all possible information about an asset is immediately priced into the asset once the information becomes available. This tends to fail because some investors get the information earlier or respond to it in different manners, so there is an inherent asymmetric incorporation of information that creates shortterm price trends (momentum) that can be exposed. This phenomenon can be further explored in Momentum. Though momentum investing is gaining in popularity, there are countless other investment strategies in use today. Value and growth investing are both examples, and view functions incorporating these strategies are an interesting topic of further research. III. Theoretical FrameworkBaselineAs mentioned in the literature review, Markowitz specifies a mean-variance utility function with respect to the portfolio asset weight vector, w. The investor's goal is to maximize the expected return while minimizing the volatility and he does so by maximizing the utility function where RT is the current period?s return, RT+1 is the future period?s return, γ is the investor?s risk aversion coefficient, μ is the sample return vector and Σ is the sample covariance matrix. This is referred to as a two moment utility function since it incorporates the distribution's first two moments, the mean and variance. The first order condition of this utility function, with respect to w, solves to which can be used to solve for the optimal portfolio weights given the historical data. BL first specify their model by determining the expected market equilibrium returns. To do so, they solve for μ in (2) by plugging in the sample covariance matrix and the market equilibrium weights. The sample covariance matrix comes from the data and the market equilibrium weights are simply the percentage that each country's market capitalization makes up of the total portfolio market capitalization. In equilibrium, if we assume that the CAPM holds and that all investors have the same risk aversion and views on the market, the demand for any asset will be equal to the available supply. The supply of an asset is simply its market capitalization, or the amount of dollars available of the asset in the market. In equilibrium when supply equals demand, we know that the weights of each asset in the optimal portfolio will be equal to the supply, or the market capitalization of each asset. Σ is simply the historical covariance matrix, so we therefore know both w and Σ in (2), meaning we can solve for μe, the equilibrium expected excess returns. It is also assumed that the true expected excess return, μ, is normally distributed with mean μe and covariance matrix τΣ. This can be written as where μe is the market equilibrium returns, τ is a scalar indicating the confidence of how the true expected returns are modeled by the market equilibrium, and Σ is the fixed sample covariance matrix. It is common practice to use a small value of tau since one would guess that long-term equilibrium returns are less volatile than historical returns. We must also incorporate the investor?s views, which can be modeled by where P is a K × N matrix that specifies K views on the N assets, and Ω is the covariance matrix explaining the degree of confidence that the investor has in his views. Ω is one of the harder variables to specify in the model, but [?] provide a method that also helps with the specification of τ. Ω is a diagonal matrix since it is assumed that views are independent of one another, meaning all covariance (non-diagonal) elements of the matrix are zero. Each diagonal element of Ω can be thought of as the variance of the error term, which can be specified as PiΣP'0i, where Pi is an individual row (view) from the K × N view specifying matrix, and Σ is again the historical covariance matrix. Again, I do not agree with this overemphasis on the historical covariance matrix, but I include it here for simplicity of explaining the intuition of the model. Intuition calibrate the confidence of each view by shrinking each view's error team by multiplying it by τ. This makes τ independent of the posterior analysis because it is now incorporated in the same manner in the two stages of the model. If it is drastically increased, so too are be the error terms of Ω, but the estimated return vector, shown in (5) is not changed because there is be an identical effect on Σ. We can combine these two models by Bayesian updating, which leaves us with the Black-Litterman mean and variance The Black-Litterman posterior covariance matrix is simply [(τΣh)−1+P'Ω−1P]−1. The extra addition of Σ occurs because the investor must account for the added uncertainty of making a future prediction. This final distribution is referred to as the posterior predictive distribution and is derived through Bayesian updating. There is an added uncertainty in making a prediction of an unknown, future value, and to account for this the addition of Σ is necessary. It is assumed that both the market equilibrium and the investor?s views follow a multivariate normal distribution, so it is known that the posterior predictive distribution is also multivariate normal due to conjugacy. In order to find the optimal portfolio weights μBL and ΣBL are simply plugged into (2). Once the Black-Litterman results are specified we have the joint prior for the Bayesian extension. We combine this prior with the normal likelihood function describing the data4, and based off of Bayesian updating logic we obtain the posterior predictive mean, μbayes and covariance matrix, Σbayes, where Σ is the historical covariance matrix, μh are the historical means of the asset returns, Δ = (τΣ)−1+P'Ω−1P]−1 is the covariance matrix of the Black-Litterman estimate, and T is the sample size of the data, which is the weight prescribed to the sample data. The larger the sample size chosen, the larger the weight the data has in the results. It is common practice to let T = n, unless we do not have a high level of confidence in the data and want T <n. The number of returns is specified independently from the data because only the sample mean and covariance matrix are used in the analysis, not the individual returns. This is ideal because it allows the investor to set the confidence in the data without the sample size doing it automatically. Historical return data is often lengthy, but that does not necessarily mean a high degree of confidence should be prescribed to it. Analogous to the Black-Litterman model, the posterior estimate of Σ in Zhou is [(Δ−1 +(Σ/T )−1]−1. The addition of Σ to the posterior in calculating Σbayes is necessary to account for the added uncertainty of the posterior predictive distribution. The theory behind this is identical to that in the Black-Litterman model. It is known that both the prior and likelihood follow a multivariate normal distribution, so due to conjugacy the same is true of the posterior predictive distribution. The posterior mean is a weighted average of the Black-Litterman returns and the historical means of the asset returns. As the sample size increases, so does the weight of the historical returns in the posterior mean. In the limit if T = ∞, then the portfolio weights are identical to the mean-variance weights, and if T = 0 then the weights are identical to the Black-Litterman weights. ExtensionAs it stands, the Zhou model uses the sample covariance matrix in the prior generating stage, even though in a fully Bayesian analysis a full incorporation of historical data is not supposed to occur outside of the likelihood function. This means the data is used to generate the prior views, and then further update the views by again incorporating the data through the likelihood function. To account for the uncertainty of modeling Σ under the historical covariance matrix in each stage, I will impose an inverse-Wishart prior on the Black-Litterman covariance matrix. Under this method, the historical covariance matrix will still be used in both Bayesian updating stages, but I can now better account for the potential problems of doing so through the inverse-Wishart prior. The inverse-Wishart prior changes only the specification of Σ , not μ, and is specified by W−1(Ψ, v.0) where Ψ is the prior mean of the covariance matrix, and v.0 is the degrees of freedom of the distribution. The larger the degrees of freedom, the more confidence the investor has in Ψ as an estimate of Σ. In this case, Ψ = ΣBL, and v.0 can be thought of as the number of "observations" that went into the prior5. The prior is then updated by the likelihood function, the historical estimate of Σ. μBL is also updated by the historical data, but the analysis does not change the specification of μ since the prior is only put on the ΣBL. The posterior distribution of Σ is also an inverse-Wishart distribution due to the conjugate Bayesian update and is defined as W−1((Ψ+Sμ), (v.0+T)), where Sμ is the historical data generated sum of squares matrix, and T the number of observations that were used to form the likelihood. T is specified in the same manner as in the Zhou model; it is up to the investor to set confidence in the data through T as it does not necessarily need to be the actual number of observations. I use the mean of the posterior inverse-Wishart distribution to define the posterior covariance matrix of the extension. The mean of the posterior is defined as E[Σ|μ, y1, ..., yn] = 1/v.0+T−n−1(Ψ+Sμ), where y1, ..., yn is the observed data, and n is the number of potential assets in the portfolio. This posterior matrix is then added to the historical covariance matrix in order to get the posterior predictive value, σext. The specification of μ is not affected under this model so μext = μbayes IV. DataMonthly dollar returns from 1970-2013, for the countries in question6 were obtained from Global Financial Data, and I used that raw data to calculate the n = 528 monthly percent returns. The analysis is based on excess returns, so assuming the investor is from the U.S. I use the 3-month U.S. Treasury bill return as the risk-free rate. Data must also be incorporated to describe the market equilibrium state of the portfolio. I collected this data from Global Financial Data and am using the market capitalizations of the entire stock markets in each country from January, 1980 to December, 2013. Given the rolling window used in my analysis, January, 1980 is the first month where market equilibrium data is needed Table 1 presents descriptive statistics for the seven country indices I am analyzing. The mean annualized monthly excess returns are all close to seven percent and the standard deviations are all close to 20 percent. The standard deviation for the U.S. is much smaller than the other countries, which makes sense because safer investments generally have less volatility in returns. All countries exhibit relatively low skewness, and most countries have a kurtosis that is not much larger than the normal distributions kurtosis of 3. The U.K. deviates the most from the normality assumption given it has the largest absolute value of skewness and a kurtosis that is almost two times as large as the next largest kurtosis. I am not particularly concerned by these values, however, because the dataset is large and the countries do not drastically differ from a normal distribution. The U.K. is the most concerning, but a very large kurtosis is less problematic than a very large skewness and the skewness is greatly influenced by one particularly large observation that occurred in January of 1975, during a recession. Though the observation is an outlier, it seems to have occurred under legitimate circumstances so I include it in the analysis. V. Model ImplementationRolling WindowA predictive model is best tested under repeated conditions when it uses a subset of the data as "in-sample" data to predict the "out-of sample" returns. This simulates how a model would be implemented in a real investment setting since there is obviously no data incorporated in the model for the future prediction period. If I were to include the observations I was also trying to predict, I would artificially be increasing the predictive power of the model by predicting inputs. I am using a 10 year rolling window as the in sample data to predict the following month. I begin with the first 10 years of the dataset, January, 1970 December, 1980, to predict returns and optimal asset weights for the following month, January 1981. I then slide the window over one month and use February, 1970 January, 1981 to predict returns and optimal asset allocations for February, 1981. The dataset spans through 2013, giving me 528 individual returns. I therefore calculate 408 expected returns and optimal weights. It is quite easy to assess performance once each set of optimal weights is calculated since there is data on each realized return. For each iteration I calculate the realized return for the entire portfolio by multiplying each individual index's weight by its corresponding realized return. I do not have any investment constraints in the model so I also need to account for the amount invested in, or borrowed from, the risk-free rate. One minus the sum of the portfolio weights is the amount invested in (or borrowed from, if negative) the risk-free rate. Momentum Based viewsIn order to be able to run the model in an updating fashion, I must to create a function that will iteratively specify the investor's views, and I will do so using a momentum based investment strategy. I have created a function that uses both a primary absolute strategy and a secondary relative strategy that is explained below. The primary strategy estimates absolute views based on the mean and variance of the previous twelve months, since this is the known window for Momentum. This is a loose adaption of our momentum strategy that specifies that stocks that have performed well in the past twelve months will continue to do so in the following month. By taking the mean I can account for the fact that at many times, the indices have no momentum, in which case I expect the mean to be close to zero. For this strategy, since I am only specifying absolute views, the P matrix is an identity matrix with a dimension equal to the number of assets in question. The Omega matrix is again calculated using the method specified by Intuition. The secondary strategy, which is appended to both of these primary strategies, if the conditions hold, attempts to find indices that are gaining momentum quickly in the short term. To do this I look at the last 4 months of the returns to see if they are consistently increasing or decreasing. If the index is increasing over the four months, it is given a positive weight, and if it is decreasing over the four months it is given a negative weight. I use a four-month increasing scheme to catch the indices under momentum before they hit the standard six-month cutoff. The weights are determined by a method similar to the market capitalization weighting method used by Idzorek. The over-performing assets are weighted by the ratio of the individual market capitalization to the total over-performing market capitalization, and the same goes for under-performing assets. This puts more weight on large indices, which is intuitive because there is likely more potential for realized returns in this case. The expected return of this view is a market capitalization weighted mean of each of the indices that have the specified momentum. This is a fairly strict strategy, which is why I refer to it as secondary. For each iteration, sometimes there are no underperforming or over performing assets under the specifications. In this case, only the primary strategy is used. If assets do appear to have momentum given the definition, then it is appended to the P matrix along with the primary strategy. VI. ResultsThe results of the four models are presented below in Table 2. It must be considered that the results are heavily dependent on the dataset and the view specifying function, two aspects of the model that are not necessarily generalizable to an investor. Further empirical analysis of the models is therefore necessary to determine which is best under the varying conditions of the current investment market. The Markowitz model performs the worst of the models, both in terms of volatility and returns. A high volatility implies that the returns for each iteration are not consistent, which is a known feature of the Markowitz model. The results also imply that given the dataset, the historical mean and covariance do not do a great job on their own as data inputs in the portfolio optimization problem. This is consistent with the original hypothesis that further data inputs are necessary in conjunction with a more robust modeling procedure to improve the overall model. The Black-Litterman model outperforms the Zhou model in both returns and volatility, meaning that in this analysis the incorporation of the historical data is not optimal. However, this does not render the Zhou model useless since repeated empirical analysis is necessary to determine the actual effects of the historical data. In Zhou only one iteration of the model is run as brief example, so there is currently no sufficient literature on whether the historical data is an optimal addition. A robust model testing procedure could be employed by running a rolling-window model testing procedure on many datasets, and then running t-tests on the set of returns and volatilities specified under each dataset to find if one model outperforms the other. The inverse-Wishart prior performs significantly better than in volatility than all the other models, and is only beaten by the Black-Litterman model in returns. This is in line with the hypothesis that the inverse-Wishart prior will better specify the covariance matrix which will in turn lead to safer investment positions. Low volatility portfolios generally do not have high returns, and given that the volatility of the extension is so much lower than the Black-Litterman volatility, it is not surprising that the return is also lower. VII. DiscussionIn exploring the results of the extended Zhou model it is clear that fully Bayesian models are able to outperform models that use loosely Bayesian methods. The inverse-Wishart extension outperforms the Zhou model in portfolio volatility by accounting for the uncertainty of modeling Σ and by allowing the investor to further specify confidence in the Black-Litterman and historical estimates. The parameters are straightforward and determined by the investor's confidence in each data input, which makes the model relatively simple and usable by any type of investor. The Black-Litterman model, which is used as a joint prior in extended model, allows the investor to incorporate any sort of views on the market. The views can be determined in a oneoff nature views or by a complex iterative function specifying a specific investment strategy. The former would likely be employed by an amateur, independent investor while the latter by a professional or investment team. The data updating stage has similar flexibility in that the historical means, or a more complex data modeling mechanism, can be employed depending on the quantitative skills of the investor. The incorporation of a predictive model is a topic of further research that could significantly increase the profitability of the Bayesian model, though it would also greatly increase the complexity. Asset return predictions models can also be incorporated in a much simpler manner through the use of absolute views. The inverse-Wishart prior is used to model the uncertainty of predicting the next period's covariance matrix, which is not fully accounted for in the original Zhou model. This method works well empirically in this analysis, but further empirical testing is necessary to see if it consistently out-performs the Zhou model. A further extension that could account for the problems in modeling Σ is through use a different estimate of Σ in the equilibrium stage, rather than just the historical covariance. When many assets are being analyzed, the historical covariance matrix does estimate Σ well, so using another method of prediction could be very useful. Factor and stochastic volatility models could both provide another robust estimate of Σ in the equilibrium stage. Another possible extension that is possible under the inverseWishart prior is to fully model the posterior predictive distribution, rather than simply using the mean value of the posterior inverse-Wishart distribution as the posterior estimate. The posterior predictive distribution under the inverseWishart prior is t-distributed, which may also be useful the since financial data is known to have fatter tails than the normal distribution. This would greatly increase the complexity of the model, however, since the expected utility would need to be maximized with respect to the posterior t-distribution, and this can only be done through complex integration. The results presented in this paper give an idea of how the models perform under repeated conditions through the use of the rolling window. However, each iteration of the rolling window is very similar to the previous one since all but one data point is identical. In order to confidently determine if one model outperforms another, it is necessary to do an empirical analysis on multiple datasets. As exemplified above, an investor can use many different strategies to specify the views, expected returns, and expected covariance matrix incorporated in the model. The method of combining these estimates is also quite important as seen by the optimal performance of the extended model, which used the same data inputs but incorporated an inverse-Wishart prior. By using Bayesian strategies to combine these different methods of prediction with the market equilibrium returns, the investor has a straightforward quantitative model that can help improve investment success. Almost all investors base their decisions off how they view the assets in the market, and by using this model, or variations of it, they can greatly improve their chance of profitability by using robust methods of prediction. References
Footnotes
Suggested Reading from Inquiries Journal
Inquiries Journal provides undergraduate and graduate students around the world a platform for the wide dissemination of academic work over a range of core disciplines. Representing the work of students from hundreds of institutions around the globe, Inquiries Journal's large database of academic articles is completely free. Learn more | Blog | Submit Latest in Economics |